(2020 - Now) Overparametrization, generalization and robustness
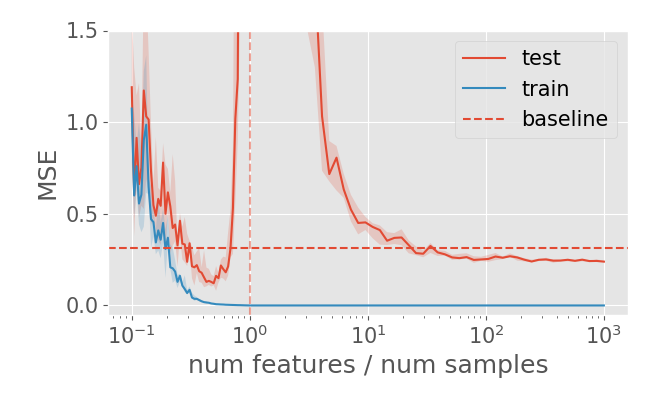
Along the last decade, machine learning underwent many breakthroughs, usually led by empirical improvements that allowed very large models to perform well and attain state-of-the-art performance on tasks ranging from image classification to playing online games. These models, however, often have millions or, even, billions of parameters. Parsimoniousness is a key principle in the philosophy behind science and engineering and it is often pursued in popular machine learning and statistical methods (ideas about pruning, distilling or building sparse neural networks are popular as it is, in a more classical setting, the idea of selecting a subset of regressors). The traditional bias-variance trade-off can be thought of as a formalization of this principle in probabilistic terms. However, as the bias-variance trade-off gets revisited, with the study of overparametrized models and the observation of a second descent in the risk as we increase the model capacity beyond the point of (almost) perfectly fitting the training data, one might wonder if there are other instances of how the models are evaluated where parsimonious models are still the best alternative. My most recent line of research focus on the interplay between overparametrization and generalization studying how different overparamentrized models generalize. With two special focus: the first is how dynamic models generalize and the second is how robust to out-of-distribution scenarios overparametrized models are. Indeed, robustness is a fundamental goal in machine learning. In many situations, the data distribution observed in using the final model is not exactly the same as the one used to develop the model. Furthermore, the ability to generalize to out-of-distribution scenarios is an important capability for the successful deployment of these models. Indeed, it has recently been observed that the interplay between overparametrization and robustness might be a key question for the deployment of modern machine learning models.
Selected publications:
- Beyond Occam's Razor in System Identification: Double-Descent when Modeling Dynamics (2021). Proceedings of the 19th IFAC Symposium on System Identification (SYSID) - IFAC-PapersOnLine. Antônio H. Ribeiro, Johannes N. Hendriks, Adrian G. Wills, Thomas B. Schön
- Overparametrized Regression Under L2 Adversarial Attacks (2021). Workshop on the Theory of Overparameterized Machine Learning (TOPML). Antonio H Ribeiro, Thomas B Schön
- Beyond Occam's Razor in System Identification: Double-Descent when Modeling Dynamics (2021). Workshop on Nonlinear System Identification. Antônio H. Ribeiro, Johannes N. Hendriks, Adrian G. Wills, Thomas B. Schön
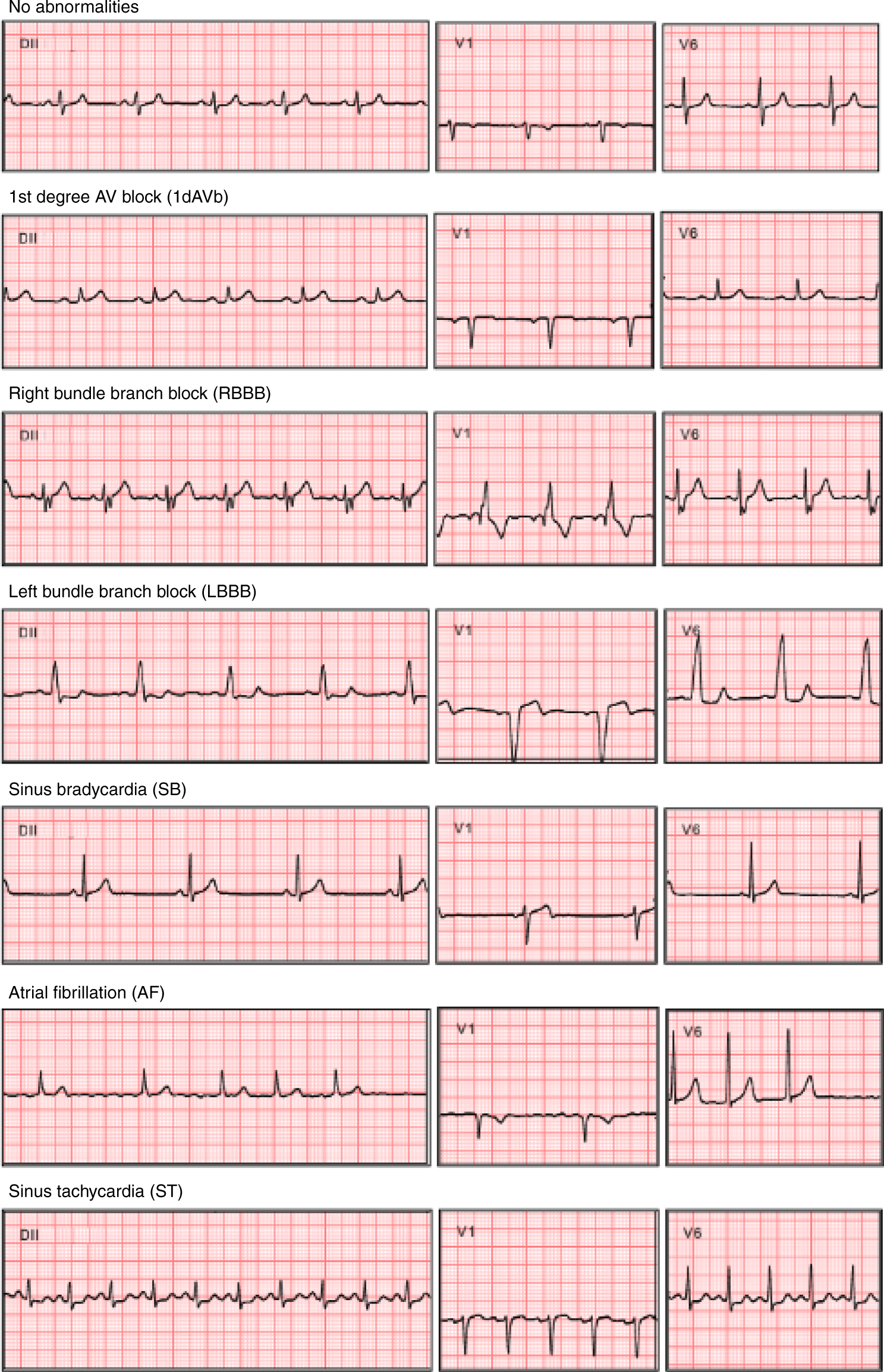The electrocardiogram is a medical test used to measure cardiac electrical activity, being the most common complementary exam to assess the heart condition. My current research leverages the latest developments in machine learning for extending and improving how ECG is used in clinical practice. My involvement with ECG analysis started in 2018 when I joined the research group CODE (Clinical Outcomes in Electrocardiography) at Universidade Federal de Minas Gerais. Using a dataset with more then 2 million entries collected and annotated between 2010 to 2017 by the Telehealth Network of Minas Gerais we developed a system capable of detecting some ECG abnormalities with greater accuracy then cardiology residents. After this successful proof of concept project, I am now involved on diverse projects using AI for ECG analysis including: the prediction of age from the ECG and its use for improving risk assessment; the creation of tools to detect Atrial Fibrillation before its development; and, tools for detecting non-ST segment elevation myocardial infarction. Now, working not only with data from Brazil, but also, since 2021, with the Clinical Epidemiology Unit in Uppsala University to power new AI applications for ECG analysis using more than one million ECG collected in Stockholm region between 2007 and 2016.
Mathematical models of dynamic systems are of fundamental importance for science and engineering. Linear models of dynamic systems are well understood and are the standard choice for most engineering applications. However, pushing the forefront of current engineering technology requires us to better understand, model, and control nonlinear systems. Applications range from using flexible wings for building more efficient airplanes to using amplifiers near the saturation region to meet the needs of the future generation of wireless communication. My research focus on analysing and developing new methods for identifying dynamical systems and learning its behavior from empirical data. This was the theme of my Master's and Ph.D. Thesis and a topic of current research.
A stereo camera is a camera that captures two (or more images) simultaneously from different viewpoints for the purpose of estimating depth. The idea mimics our own eyes, which give us a sense of depth precisely because they capture two simultaneous images from different points of view. I worked in all stages of the development of stereo camera based on FPGA technology, from the image acquisition from an image sensor through an FPGA chip to the several steps required to estimate the depth of a scene using a stereo camera: calibration (determination of geometry and parameters of the stereo camera); rectification (alignment of the images); correspondence (determination of the corresponding points in the two images and the distance between them); and, reconstruction (calculating the position of objects by triangulation). The project was develop during my internship at Invent Vision development team. The company develops cameras and provides computer vision solutions for industry. At that point the company was commissioned to make a decoking monitoring system at an oil refinery. For this task, it was interesting to have a cloud of points containing the internal structure of the refinery drum, which sparked the company's interest in stereo vision technology. Working there, I developed a prototype of a stereo camera which is described in a monograph I wrote during my undergraduate course as requirement for obtaing the Bachelor degree in Electrical Engineering.
In offshore oil extraction, the instruments located at the bottom of the well undergo a rapid wear due to extreme conditions. The maintenance and exchange of such equipment is complicated and expensive. In this context, obtaining mathematical models for variables at the bottom of the oil well from platform variables is a simple and inexpensive solution. These mathematical models are also called virtual sensors. As a undergraduate student, I participated on a research and development project coordinated by professor Luis Antônio Aguirre fromm Universidade Federal de Minas Gerais (Brasil) together with Petrobras Oil Company together for the development of virtual sensors from historical data of the oil well operation. These virtual sensors could replace the measurement instrumented located at the bottom of the production column in offshore oil extraction temporarily in case of malfunctioning.